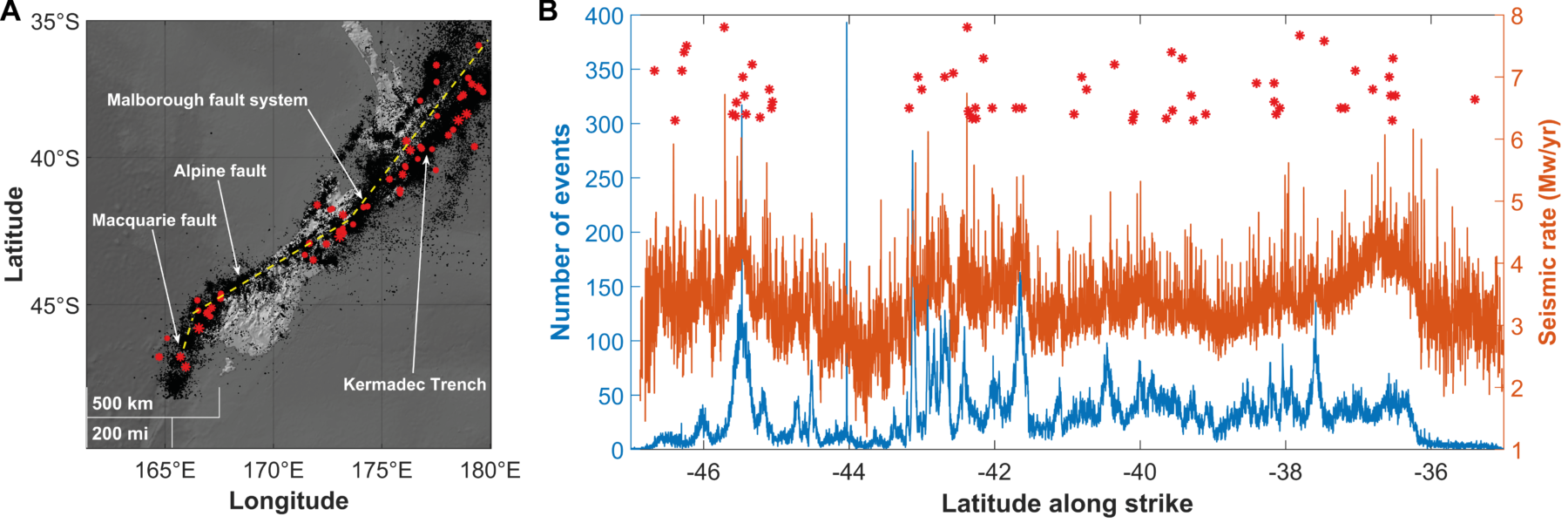
Clustering is the essence of earthquake occurrence. Although not exhaustive, our analysis is a first attempt to understand what information may be hidden in partial, limited earthquake catalogs only containing mid-size and a few large seismic events (or even no one) about the largest possible ones. We consider the local and global coefficients of variation, the scaling exponent of the Gutenberg–Richter law, the fractal dimension of epicentral series D𝑓 , the seismic rate and the number of events. We find that the largest earthquakes occur in locally Poissonian systems (L𝑉 ≈ 1) with globally clustered dynamics (C𝑉 > 1). What is more interesting, we highlight that, while the local clustering behavior is strongly dependent on the size of catalog, so that longer databases tend to be less regular and more Poissonian than shorter ones, the global coefficient seems to be a reliable parameter even in cases of rather limited available information (few thousand events). This observation can be explained in the light of self-similar dynamics, so, analogous patterns producing both intermediate, large and extreme earthquakes. The fractal dimension of spatial series is positively correlated with the seismic rate, C𝑉 and, therefore, with the maximum observed magnitude in catalog. Conversely, the 𝑏-value does not show any correlation with the principal observables except for the number of earthquakes. This phenomenon is due to the different sizes of mainshocks in various tectonic settings, namely higher in thrust-faulting than strike-slip- and normal-faulting regions, which are known to be characterized, respectively, by increasing 𝑏-values. Further research must be done in order to understand the real potential of these statistical parameters in the field of earthquake forecasting. We propose that their predictive power stems from the self-similar nature of slow dynamics producing the emergence of avalanches and breakdown in complex systems such as the brittle crust. In the light of this, global observables are the best candidates for modeling the long-term physical processes ultimately responsible for large earthquakes. By a physical viewpoint, they are also the most appropriate to grab and to describe mathematically the long-range interactions developing in disordered and critical settings while approaching dynamical transitions. So, our attention should be drawn to find new global collective observables showing predictive power and to apply them in order to set up new models of earthquake occurrence. Prospectively, this approach can be of great interest, once tuned, to extrapolate the features of extreme, still unobserved events given a limited database.
https://www.sciencedirect.com/science/article/pii/S096007792300320X